Electron. J. Differential Equations,
Vol. 2017 (2017), No. 141, pp. 1-13.
Existence and asymptotic behavior of positive solutions for
semilinear fractional Navier boundary-value problems
Habib Maagli, Abdelwaheb Dhifli
Abstract:
We study the existence, uniqueness, and asymptotic
behavior of positive continuous solutions to the fractional Navier
boundary-value problem
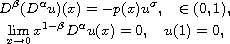
where
![$\alpha ,\beta \in (0,1]$](gifs/ab.gif) such that
such that
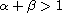 ,
,
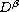 and
and
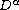 stand for the standard Riemann-Liouville fractional
derivatives,
stand for the standard Riemann-Liouville fractional
derivatives,
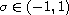 and p being a nonnegative continuous
function in (0,1) that may be singular at x=0 and satisfies some
conditions related to the Karamata regular variation theory. Our approach is
based on the Schauder fixed point theorem.
and p being a nonnegative continuous
function in (0,1) that may be singular at x=0 and satisfies some
conditions related to the Karamata regular variation theory. Our approach is
based on the Schauder fixed point theorem.
Submitted February 11, 2017. Published May 25, 2017.
Math Subject Classifications: 34A08, 34B15, 34B18, 34B27.
Key Words: Fractional Navier differential equations; Dirichlet problem;
positive solution; asymptotic behavior; Schauder fixed point theorem.
Show me the PDF file (254 KB),
TEX file for this article.
 |
Habib Mâagli
King Abdulaziz University, Rabigh Campus
College of Sciences and Arts
Department of Mathematics, P.O. Box 344
Rabigh 21911, Saudi Arabia
email: habib.maagli@fst.rnu.tn
|
|---|
 |
Abdelwaheb Dhifli
Département de Mathématiques
Faculté des Sciences de Tunis
Campus Universitaire
2092 Tunis, Tunisia
email: dhifli_waheb@yahoo.fr
|
|---|
Return to the EJDE web page
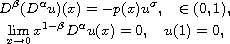
![$\alpha ,\beta \in (0,1]$](gifs/ab.gif) such that
such that
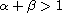 ,
,
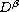 and
and
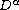 stand for the standard Riemann-Liouville fractional
derivatives,
stand for the standard Riemann-Liouville fractional
derivatives,
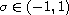 and p being a nonnegative continuous
function in (0,1) that may be singular at x=0 and satisfies some
conditions related to the Karamata regular variation theory. Our approach is
based on the Schauder fixed point theorem.
and p being a nonnegative continuous
function in (0,1) that may be singular at x=0 and satisfies some
conditions related to the Karamata regular variation theory. Our approach is
based on the Schauder fixed point theorem.

