Electron. J. Differential Equations,
Vol. 2017 (2017), No. 13, pp. 1-15.
Well-posedness of weak solutions to electrorheological fluid equations with
degeneracy on the boundary
Huashui Zhan, Jie Wen
Abstract:
In this article we study the electrorheological fluid equation
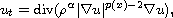
where
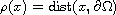 is the distance from the boundary,
is the distance from the boundary,
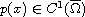 ,
and
,
and
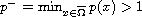 .
We show how the degeneracy of
.
We show how the degeneracy of
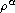 on the boundary affects the well-posedness of the weak solutions.
In particular, the local stability of the weak solutions is
established without
any boundary value condition.
on the boundary affects the well-posedness of the weak solutions.
In particular, the local stability of the weak solutions is
established without
any boundary value condition.
Submitted August 12, 2016. Published January 12, 2017.
Math Subject Classifications: 35L65, 35K85, 35R35.
Key Words: Electrorheological fluid equation; boundary degeneracy;
Holder's inequality; local stability.
Show me the PDF file (287 KB),
TEX file for this article.
 |
Huashui Zhan
School of Applied Mathematics
Xiamen University of Technology
Xiamen, Fujian 361024, China
email: 2012111007@xmut.edu.cn
|
|---|
 |
Jie Wen
School of Sciences
Jimei University
Xiamen, Fujian 361021, China
email: 1195103523@qq.com
|
|---|
Return to the EJDE web page
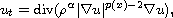
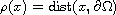 is the distance from the boundary,
is the distance from the boundary,
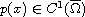 ,
and
,
and
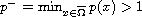 .
We show how the degeneracy of
.
We show how the degeneracy of
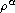 on the boundary affects the well-posedness of the weak solutions.
In particular, the local stability of the weak solutions is
established without
any boundary value condition.
on the boundary affects the well-posedness of the weak solutions.
In particular, the local stability of the weak solutions is
established without
any boundary value condition.

