This article concerns the SIRC epidemiological model for influenza A, which efficiently describes the mechanism of disease spreading, including the susceptible (S), the infected (I) and the recovered (R), along with a cross-immune class (C) that recovers after being inflected by different strains of the same viral subtype. The dynamics of the model is completely determined by the basic reproduction number
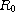 . If
. If
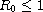 ,
the disease-free equilibrium of the SIRC
model is globally asymptotically stable, which means influenza A will die out.
Otherwise, the SIRC model may have exactly one endemic equilibrium which
is globally asymptotically stable under certain parametric conditions.
Also, numerical simulations are given to support our analytical results.
,
the disease-free equilibrium of the SIRC
model is globally asymptotically stable, which means influenza A will die out.
Otherwise, the SIRC model may have exactly one endemic equilibrium which
is globally asymptotically stable under certain parametric conditions.
Also, numerical simulations are given to support our analytical results.

