Electron. J. Differential Equations,
Vol. 2017 (2017), No. 115, pp. 1-13.
Existence of solutions for degenerate Kirchhoff type problems
with fractional p-Laplacian
Nemat Nyamoradi, Lahib Ibrahim Zaidan
Abstract:
In this article, by using the Fountain theorem and Mountain
pass theorem in critical point theory without Palais-Smale (PS)
condition, we show the existence and multiplicity of solutions
to the degenerate Kirchhoff type problem with the fractional
p-Laplacian
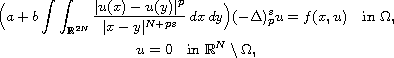
where
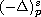 is the fractional p-Laplace operator
with
is the fractional p-Laplace operator
with
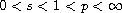 ,
,
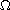 is a smooth bounded domain of
is a smooth bounded domain of
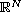 ,
N > 2 s, a, b > 0 are constants and
,
N > 2 s, a, b > 0 are constants and
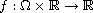 is a continuous function.
is a continuous function.
Submitted February 23, 2017. Published April 27, 2017.
Math Subject Classifications: 34B27, 35J60, 35B05.
Key Words: Kirchhoff nonlocal operators; fractional differential equations;
fountain theorem; mountain pass theorem; critical point theory.
Show me the PDF file (281 KB),
TEX file for this article.
 |
Nemat Nyamoradi
Department of Mathematics
Faculty of Sciences,
Razi University
67149 Kermanshah, Iran
email: nyamoradi@razi.ac.ir, neamat80@yahoo.com
|
|---|
 |
Lahib Ibrahim Zaidan
Department of Mathematics,
Faculty of Sciences,
Razi University
67149 Kermanshah, Iran
email: lahibzaidan75@yahoo.com; lahibzaidan@uobabylon.edu.iq
|
|---|
Return to the EJDE web page
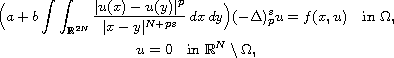
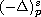 is the fractional p-Laplace operator
with
is the fractional p-Laplace operator
with
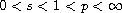 ,
,
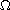 is a smooth bounded domain of
is a smooth bounded domain of
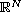 ,
N > 2 s, a, b > 0 are constants and
,
N > 2 s, a, b > 0 are constants and
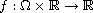 is a continuous function.
is a continuous function.

