Electron. J. Differential Equations,
Vol. 2017 (2017), No. 114, pp. 1-15.
Ground state solutions for a quasilinear Schrodinger equation
with singular coefficients
Jixiu Wang, Qi Gao, Li Wang
Abstract:
In this article, we study the quasilinear Schrodinger equation
with the critical exponent and singular coefficients,
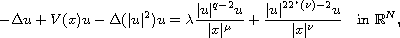
where
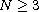 ,
,
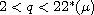 ,
,
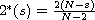 ,
and
,
and
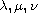 are parameters with
are parameters with
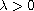 ,
,
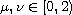 .
By applying the Mountain Pass Theorem and the Concentration
Compactness Principle, we establish the existence of the ground state solutions
to the above problem.
.
By applying the Mountain Pass Theorem and the Concentration
Compactness Principle, we establish the existence of the ground state solutions
to the above problem.
Submitted March 7, 2017. Published April 27, 2017.
Math Subject Classifications: 35J62, 35J60, 35J20.
Key Words: Quasilinear Schrodinger equations; critical exponent;
ground state solutions; calculus of variations.
Show me the PDF file (285 KB),
TEX file for this article.
 |
Jixiu Wang
School of Mathematics and Computer Science
Hubei University of Arts and Science
Xiangyang 441053, China
email: wangjixiu127@163.com
|
|---|
 |
Qi Gao
Department of Mathematics
School of Science
Wuhan University of Technology
Wuhan 430070, China
email: gaoq@whut.edu.cn
|
|---|
 |
Li Wang
College of Science
East China Jiaotong University
Nanchang 330013, China
email: wangli.423@163.com
|
|---|
Return to the EJDE web page
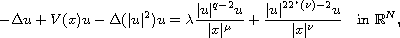
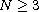 ,
,
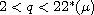 ,
,
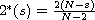 ,
and
,
and
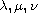 are parameters with
are parameters with
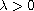 ,
,
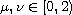 .
By applying the Mountain Pass Theorem and the Concentration
Compactness Principle, we establish the existence of the ground state solutions
to the above problem.
.
By applying the Mountain Pass Theorem and the Concentration
Compactness Principle, we establish the existence of the ground state solutions
to the above problem.


