Electron. J. Differential Equations,
Vol. 2017 (2017), No. 113, pp. 1-10.
Existence of positive solutions to nonlinear elliptic systems
involving gradient term and reaction potential
Ahmed Attar, Rachid Bentifour
Abstract:
In this note we study the elliptic system
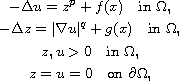
where
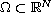 is a bounded domain, p>0,
is a bounded domain, p>0,
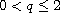 with pq<1 and f,g are two nonnegative measurable functions.
The main result of this work is to analyze the interaction between
the potential and the gradient terms in order to get the existence
of a positive solution.
with pq<1 and f,g are two nonnegative measurable functions.
The main result of this work is to analyze the interaction between
the potential and the gradient terms in order to get the existence
of a positive solution.
Submitted July 6, 2016. Published April 26, 2017.
Math Subject Classifications: 35K15, 35K55, 35K65, 35B05, 35B40.
Key Words: Elliptic system; Schauder fixed point theorem; gradient dependance.
Show me the PDF file (230 KB),
TEX file for this article.
 |
Ahmed Attar
Laboratoire d'Analyse Nonlinéaire et Mathématiques Appliquées
Département de
Mathématiques
Université Abou Bakr Belkaïd, Tlemcen
Tlemcen 13000, Algeria
email: ahm.attar@yahoo.fr
|
|---|
 |
Rachid Bentifour
Laboratoire d'Analyse Nonlinéaire et Mathématiques Appliquées
Département de
Mathématiques
Université Abou Bakr Belkaïd, Tlemcen
Tlemcen 13000, Algeria
email: rachidbentifour@gmail.com
|
|---|
Return to the EJDE web page
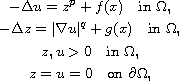
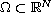 is a bounded domain, p>0,
is a bounded domain, p>0,
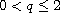 with pq<1 and f,g are two nonnegative measurable functions.
The main result of this work is to analyze the interaction between
the potential and the gradient terms in order to get the existence
of a positive solution.
with pq<1 and f,g are two nonnegative measurable functions.
The main result of this work is to analyze the interaction between
the potential and the gradient terms in order to get the existence
of a positive solution.

