Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 97, pp. 1-11.
Multiple solutions for critical elliptic problems with fractional Laplacian
Guowei Lin, Xiongjun Zheng
Abstract:
This article is devoted to the study of the nonlocal fractional equation
involving critical nonlinearities
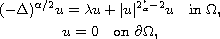
where
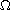 is a smooth bounded domain of
is a smooth bounded domain of
 ,
,
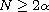 ,
,
 ,
,
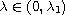 and
and
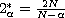 is critical exponent.
We show the existence of at least
is critical exponent.
We show the existence of at least
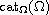 nontrivial solutions for this problem.
nontrivial solutions for this problem.
Submitted January 11, 2016. Published April 14, 2016.
Math Subject Classifications: 35J60, 35J61, 35J70, 35J99.
Key Words: Fractional Laplacian, critical exponent, multiple solutions, category.
Show me the PDF file (241 KB),
TEX file for this article.
 |
Guowei Lin
Department of Mathematics
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: lgw2008@sina.cn
|
|---|
 |
Xiongjun Zheng
Department of Mathematics
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: xjzh1985@126.com
|
|---|
Return to the EJDE web page
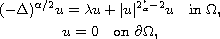
 is a smooth bounded domain of
is a smooth bounded domain of
 ,
,
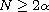 ,
,
 ,
,
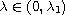 and
and
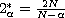 is critical exponent.
We show the existence of at least
is critical exponent.
We show the existence of at least
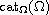 nontrivial solutions for this problem.
nontrivial solutions for this problem.

