Electron. J. Diff. Equ., Vol. 2016 (2016), No. 89, pp. 1-13.

Existence, boundary behavior and asymptotic behavior of solutions to singular elliptic boundary-value problems

Ge Gao, Baoqiang Yan

Abstract:
In this article, we consider the singular elliptic boundary-value problem
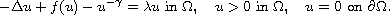
$$ -\Delta u+f(u)-u^{-\gamma} =\lambda u \text{ in } \Omega,\quad u>0\text{ in } \Omega,\quad u=0 \text{ on } \partial\Omega. $$
Using the upper-lower solution method, we show the existence and uniqueness of the solution. Also we study the boundary behavior and asymptotic behavior of the positive solutions.

Submitted November 6, 2015. Published March 31, 2016.
Math Subject Classifications: 35J25, 35J60, 35J75.
Key Words: 35J25, 35J60, 35J75.

Show me the PDF file (242 KB), TEX file for this article.

Ge Gao
School of Mathematical Sciences
Shandong Normal University
Jinan 250014, China
email: gaoge_jianxin@163.com
Baoqiang Yan
School of Mathematical Sciences
Shandong Normal University
Jinan 250014, China
email: yanbqcn@aliyun.com

Return to the EJDE web page