

Caisheng Chen
Abstract:
Using variational methods we prove the existence of infinitely
many solutions to the fractional Schrodinger equation

where
 .
.
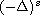 stands for the fractional
Laplacian. The potential function satisfies
stands for the fractional
Laplacian. The potential function satisfies
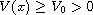 .
The nonlinearity f(x,u) is superlinear, has subcritical
growth in u, and may or may not satisfy the (AR) condition.
.
The nonlinearity f(x,u) is superlinear, has subcritical
growth in u, and may or may not satisfy the (AR) condition.
Submitted January 31, 2016. Published March 30, 2016.
Math Subject Classifications: 35R11, 35A15, 35J60, 47G20.
Key Words: Fractional Schrodinger equation; variational methods;
(PS) condition; (C)c condition
Show me the PDF file (295 KB), TEX file, and other files for this article.
 |
Caisheng Chen College of Science, Hohai University Nanjing 210098, China email: cshengchen@hhu.edu.cn |
|---|
Return to the EJDE web page