Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 80, pp. 1-14.
Uniform convergence of the spectral expansions in terms
of root functions for a spectral problem
Nazim B. Kerimov, Sertac Goktas, Emir A. Maris
Abstract:
In this article, we consider the spectral problem

where
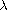 is a spectral parameter, a and b are real
constants and a<0, q(x) is a real-valued continuous
function on the interval [0,1]. The root function
system of this problem can also consist of associated functions.
We investigate the uniform convergence of the spectral expansions in terms
of root functions.
is a spectral parameter, a and b are real
constants and a<0, q(x) is a real-valued continuous
function on the interval [0,1]. The root function
system of this problem can also consist of associated functions.
We investigate the uniform convergence of the spectral expansions in terms
of root functions.
Submitted February 22, 2016. Published March 18, 2016.
Math Subject Classifications: 34B05, 34B24, 34L10, 34L20.
Key Words: Differential Operator; eigenvalues; root functions;
uniform convergence of spectral expansion.
Show me the PDF file (256 KB),
TEX file for this article.
 |
Nazim B. Kerimov
Department of Mathematics
Mersin University
33343, Mersin, Turkey
email: nazimkerimov@yahoo.com
|
|---|
 |
Sertac Goktas
Department of Mathematics
Mersin University
33343, Mersin, Turkey
email: srtcgoktas@gmail.com
|
|---|
 |
Emir A. Maris
Department of Mathematics
Mersin University
33343, Mersin, Turkey
email: ealimaris@gmail.com
|
|---|
Return to the EJDE web page

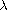 is a spectral parameter, a and b are real
constants and a<0, q(x) is a real-valued continuous
function on the interval [0,1]. The root function
system of this problem can also consist of associated functions.
We investigate the uniform convergence of the spectral expansions in terms
of root functions.
is a spectral parameter, a and b are real
constants and a<0, q(x) is a real-valued continuous
function on the interval [0,1]. The root function
system of this problem can also consist of associated functions.
We investigate the uniform convergence of the spectral expansions in terms
of root functions.


