Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 77, pp. 1-11.
Entropy solutions of exterior problems for nonlinear degenerate parabolic
equations with nonhomogeneous boundary condition
Li Zhang, Ning Su
Abstract:
In this article, we consider the exterior problem for the nonlinear degenerate
parabolic equation

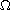 is the exterior domain of
is the exterior domain of
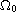 (a closed bounded domain in
(a closed bounded domain in
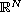 with its boundary
with its boundary
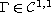 ),
),
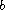 is non-decreasing and Lipschitz continuous,
is non-decreasing and Lipschitz continuous,
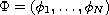 is vectorial continuous, and F is Lipschitz continuous.
In the nonhomogeneous boundary condition where
is vectorial continuous, and F is Lipschitz continuous.
In the nonhomogeneous boundary condition where
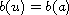 on
on
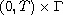 ,
we establish the comparison and uniqueness,
the existence using penalized method.
,
we establish the comparison and uniqueness,
the existence using penalized method.
Submitted January 29, 2015. Published March 18, 2016.
Math Subject Classifications: 35K55, 35K65.
Key Words: Degenerate parabolic equation; exterior problem; nonlinear;
entropy solution.
Show me the PDF file (253 KB),
TEX file for this article.
 |
Li Zhang
Management School
Hangzhou Dianzi University
Hangzhou 310018, China
email: zhli25@163.com
|
|---|
 |
Ning Su
Department of Mathematical Sciences
Tsinghua University
Beijing 100084, China
email: nsu@math.tsinghua.edu.cn
|
|---|
Return to the EJDE web page

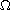 is the exterior domain of
is the exterior domain of
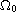 (a closed bounded domain in
(a closed bounded domain in
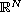 with its boundary
with its boundary
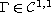 ),
),
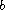 is non-decreasing and Lipschitz continuous,
is non-decreasing and Lipschitz continuous,
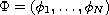 is vectorial continuous, and F is Lipschitz continuous.
In the nonhomogeneous boundary condition where
is vectorial continuous, and F is Lipschitz continuous.
In the nonhomogeneous boundary condition where
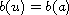 on
on
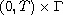 ,
we establish the comparison and uniqueness,
the existence using penalized method.
,
we establish the comparison and uniqueness,
the existence using penalized method.

