Tynysbek Sh. Kal'menov, Gaukhar D. Arepova
Abstract:
In this article, by multiplying of the unitary operator
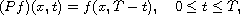
the heat potential turns into a self-adjoint operator.
From the spectral decomposition of this completely continuous
self-adjoint operator we obtain a quasi-spectral decomposition
of the heat potential operator.
Submitted January 25, 2016. Published March 17, 2016.
Math Subject Classifications: 35K05, 47F05
Key Words: Heat potential; quasi-spectral decomposition;
self-adjoint operator; unitary operator;
the fundamental solution.
Show me the PDF file (159 KB), TEX file, and other files for this article.
 |
Tynysbek Sh. Kal'menov Institute of Mathematics and Mathematical Modeling 125 Pushkin str., 050010 Almaty, Kazakhstan email: kalmenov@math.kz |
|---|---|
 |
Gaukhar D. Arepova Institute of Mathematics and Mathematical Modeling 125 Pushkin str., 050010 Almaty, Kazakhstan email: arepova@math.kz |
Return to the EJDE web page