Electron. J. Diff. Equ., Vol. 2016 (2016), No. 75, pp. 1-15.

Semi-classical states for Schrodinger-Poisson systems on R^3

Hongbo Zhu

Abstract:
In this article, we study the nonlinear Schrodinger-Poisson equation
$$\displaylines{ -\epsilon^2\Delta u+V(x) u+\phi(x)u=f(u), \quad x\in{\mathbb{R}^3}, \cr -\epsilon^2\Delta\phi=u^2,\quad \lim_{|x|\to\infty}\phi(x)=0\,. }$$
Under suitable assumptions on V(x) and f(s), we prove the existence of ground state solution around local minima of the potential V(x) as 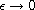$\epsilon\to 0$. Also, we show the exponential decay of ground state solution.

Submitted August 14, 2015. Published March 17, 2016.
Math Subject Classifications: 35B38, 35J20, 35J50.
Key Words: Schrodinger-Poisson system; semi-classical states; variational method.

Show me the PDF file (272 KB), TEX file for this article.

Hongbo Zhu
School of Mathematics and Statistics
Central China Normal University
Wuhan 430079, China
email: zhbxw@126.com

Return to the EJDE web page