Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 73, pp. 1-11.
Blow-up criterion for the 2D Euler-Boussinesq system in terms of temperature
Chenyin Qian
Abstract:
In this article, we study the blow-up slutions for the 2D Euler-Boussinesq
equation. In particular, it is shown that if
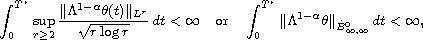
then the local solution can be continued to the global one.
This is an improvement of classical Lipschitz-type blow-up criterion
(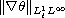 ) in terms of the
temperature
) in terms of the
temperature
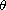 .
.
Submitted December 18, 20915. Published March 15, 2016.
Math Subject Classifications: 35Q35, 35B35, 35B65, 76D05.
Key Words: 2D Boussinesq equation; blow-up criterion; Besov space;
transport equation.
Show me the PDF file (252 KB),
TEX file for this article.
 |
Chenyin Qian
Department of Mathematics
Zhejiang Normal University
Jinhua 321004, China
email: qcyjcsx@163.com
|
|---|
Return to the EJDE web page
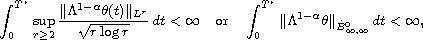
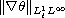 ) in terms of the
temperature
) in terms of the
temperature
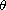 .
.
