Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 66, pp. 1-12.
Multiple homoclinic solutions for superquadratic Hamiltonian systems
Wei Jiang, Qingye Zhang
Abstract:
In this article we study the existence of infinitely many homoclinic
solutions for a class of second-order Hamiltonian systems
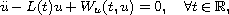
where L is not required to be either uniformly positive
definite or coercive, and W is superquadratic at infinity in u
but does not need to satisfy the Ambrosetti-Rabinowitz superquadratic condition.
Submitted December 14, 2015. Published March 10, 2016.
Math Subject Classifications: 34C37, 35A15, 37J45.
Key Words: Hamiltonian system; Homoclinic solution; variational method.
Show me the PDF file (262 KB),
TEX file for this article.
 |
Wei Jiang
Department of Mathematics
Jiangxi Normal University
Nanchang 330022, China
email: jiangweijw1991@163.com
|
|---|
 |
Qingye Zhang
Department of Mathematics
Jiangxi Normal University
Nanchang 330022, China
email: qingyezhang@gmail.com
|
|---|
Return to the EJDE web page