Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 63, pp. 1-9.
Global attractor for reaction-diffusion equations with supercritical
nonlinearity in unbounded domains
Jin Zhang, Chang Zhang, Chengkui Zhong
Abstract:
We consider the existence of global attractor for the inhomogeneous
reaction-diffusion equation
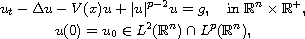
where
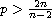 is supercritical and V(x) satisfies suitable
assumptions. Since
is supercritical and V(x) satisfies suitable
assumptions. Since
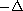 is not positive definite in
is not positive definite in
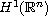 ,
the Gronwall inequality can not be derived and the corresponding semigroup
does not possess bounded absorbing sets in
,
the Gronwall inequality can not be derived and the corresponding semigroup
does not possess bounded absorbing sets in
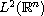 .
Thus,
by a special method, we prove that the equation has a global attractor
in
.
Thus,
by a special method, we prove that the equation has a global attractor
in
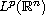 ,
which attracts any bounded subset in
,
which attracts any bounded subset in
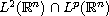 .
.
Submitted July 20, 2015. Published March 4, 2016.
Math Subject Classifications: 35B41, 35K57, 37L99.
Key Words: Global attractor; inhomogeneous reaction-diffusion equation;
unbounded domain; supercritical nonlinearity.
Show me the PDF file (232 KB),
TEX file for this article.
 |
Jin Zhang
Department of Mathematics, College of Science
Hohai University
Nanjing 210098, China
email: zhangjin86@hhu.edu.cn
|
|---|
 |
Chang Zhang
Department of Mathematics, Nanjing University
Nanjing 210093, China
email: chzhnju@126.com
|
|---|
 |
Chengkui Zhong
Department of Mathematics, Nanjing University
Nanjing 210093, China
email: ckzhong@nju.edu.cn
|
|---|
Return to the EJDE web page
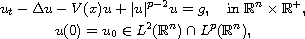
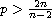 is supercritical and V(x) satisfies suitable
assumptions. Since
is supercritical and V(x) satisfies suitable
assumptions. Since
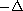 is not positive definite in
is not positive definite in
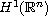 ,
the Gronwall inequality can not be derived and the corresponding semigroup
does not possess bounded absorbing sets in
,
the Gronwall inequality can not be derived and the corresponding semigroup
does not possess bounded absorbing sets in
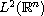 .
Thus,
by a special method, we prove that the equation has a global attractor
in
.
Thus,
by a special method, we prove that the equation has a global attractor
in
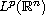 ,
which attracts any bounded subset in
,
which attracts any bounded subset in
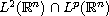 .
.


