Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 59, pp. 1-7.
Infinitely many sign-changing solutions for Kirchhoff-type
equations with power nonlinearity
Xianzhong Yao, Chunlai Mu
Abstract:
In this article we consider the Kirchhoff-type elliptic problem
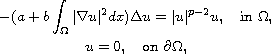
where
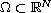 and
and
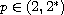 with
with
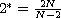 if
if
 , and
, and
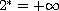 otherwise.
We show that the problem possesses infinitely many sign-changing solutions
by using combination of invariant sets of descent flow and the
Ljusternik-Schnirelman type minimax method.
otherwise.
We show that the problem possesses infinitely many sign-changing solutions
by using combination of invariant sets of descent flow and the
Ljusternik-Schnirelman type minimax method.
Submitted December 3, 2015. Published February 29, 2016.
Math Subject Classifications: 35J60, 58E05, 34C14.
Key Words: Kirchhoff-type; sign-changing solutions; invariant sets of descent flow.
An addendum was posted on April 27, 2017.
It corrects Theorem 1.1. See the last three pages of this article.
Show me the PDF file (215 KB),
TEX file for this article.
 |
Xianzhong Yao
College of Mathematics and Statistics
Chongqing University
Chongqing 401331, China
email: yaoxz416@163.com
|
|---|
 |
Chunlai Mu
College of Mathematics and Statistics
Chongqing University
Chongqing 401331, China
email: clmu2005@163.com
|
|---|
Return to the EJDE web page
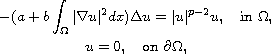
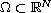 and
and
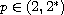 with
with
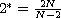 if
if
 , and
, and
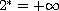 otherwise.
We show that the problem possesses infinitely many sign-changing solutions
by using combination of invariant sets of descent flow and the
Ljusternik-Schnirelman type minimax method.
otherwise.
We show that the problem possesses infinitely many sign-changing solutions
by using combination of invariant sets of descent flow and the
Ljusternik-Schnirelman type minimax method.

