Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 55, pp. 1-23.
Global structure of solutions to boundary-value problems of
impulsive differential equations
Yanmin Niu, Baoqiang Yan
Abstract:
In this article, we study the structure of global solutions to the
boundary-value problem
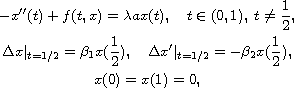
where
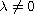 ,
,
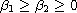 ,
,
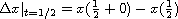 ,
,
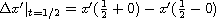 ,
and
,
and
![$f:[0,1]\times\mathbb{R}\to\mathbb{R}$](gifs/af.gif) ,
,
![$a:[0,1]\to(0,+\infty)$](gifs/ag.gif) are continuous. By a comparison principle and spectral properties
of the corresponding linear equations, we prove the existence of
solutions by using Rabinowitz-type global bifurcation
theorems, and obtain results on the behavior of positive solutions
for large
are continuous. By a comparison principle and spectral properties
of the corresponding linear equations, we prove the existence of
solutions by using Rabinowitz-type global bifurcation
theorems, and obtain results on the behavior of positive solutions
for large
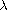 when
when
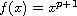 .
.
Submitted January 5, 2016. Published February 25, 2016.
Math Subject Classifications: 34B09, 34B15, 34B37.
Key Words: Comparison arguments; eigenvalues; global bifurcation theorem;
multiple solutions; asymptotical behavior of solutions.
Show me the PDF file (294 KB),
TEX file, and other files for this article.
 |
Yanmin Niu
School of Mathematical Sciences
Shandong Normal University
Jinan 250014, China
email: 1398958626@qq.com
|
|---|
 |
Baoqiang Yan
School of Mathematical Sciences
Shandong Normal University
Jinan 250014, China
email: yanbqcn@aliyun.com
|
|---|
Return to the EJDE web page
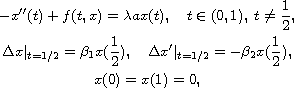
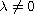 ,
,
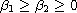 ,
,
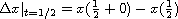 ,
,
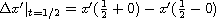 ,
and
,
and
![$f:[0,1]\times\mathbb{R}\to\mathbb{R}$](gifs/af.gif) ,
,
![$a:[0,1]\to(0,+\infty)$](gifs/ag.gif) are continuous. By a comparison principle and spectral properties
of the corresponding linear equations, we prove the existence of
solutions by using Rabinowitz-type global bifurcation
theorems, and obtain results on the behavior of positive solutions
for large
are continuous. By a comparison principle and spectral properties
of the corresponding linear equations, we prove the existence of
solutions by using Rabinowitz-type global bifurcation
theorems, and obtain results on the behavior of positive solutions
for large
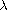 when
when
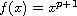 .
.

