Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 54, pp. 1-23.
Fractional elliptic equations with critical growth and
singular nonlinearities
Tuhina Mukherjee, Konijeti Sreenadh
Abstract:
In this article, we study the fractional Laplacian equation
with critical growth and singular nonlinearity

where
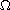 is a bounded domain in
is a bounded domain in
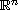 with smooth boundary
with smooth boundary
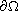 ,
,
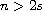 ,
,
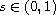 ,
,
 ,
,
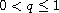 ,
,
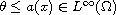 ,
for some
,
for some
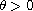 and
and
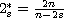 .
We use variational methods to
show the existence and multiplicity of positive solutions of the above
problem with respect to the parameter
.
We use variational methods to
show the existence and multiplicity of positive solutions of the above
problem with respect to the parameter
 .
.
Submitted December 20, 2015. Published February 23, 2016.
Math Subject Classifications: 35R11, 35R09, 35A15.
Key Words: Nonlocal operator; fractional Laplacian; singular nonlinearities.
Show me the PDF file (330 KB),
TEX file, and other files for this article.
 |
Tuhina Mukherjee
Department of Mathematics
Indian Institute of Technology Delhi
Hauz Khaz, New Delhi-16, India
email: tulimukh@gmail.com
|
|---|
 |
Konijeti Sreenadh
Department of Mathematics
Indian Institute of Technology Delhi
Hauz Khaz, New Delhi-16, India
email: sreenadh@gmail.com
|
|---|
Return to the EJDE web page

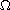 is a bounded domain in
is a bounded domain in
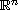 with smooth boundary
with smooth boundary
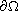 ,
,
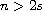 ,
,
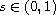 ,
,
 ,
,
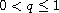 ,
,
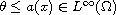 ,
for some
,
for some
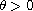 and
and
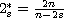 .
We use variational methods to
show the existence and multiplicity of positive solutions of the above
problem with respect to the parameter
.
We use variational methods to
show the existence and multiplicity of positive solutions of the above
problem with respect to the parameter
 .
.

