Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 51, pp. 1-8.
Positive solutions for second-order boundary-value problems with
phi-Laplacian
Diana-Raluca Herlea
Abstract:
This article concerns the existence, localization and multiplicity
of positive solutions for the boundary-value problem
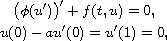
where
![$f:[0,1]\times \mathbb{R}_{+}\to \mathbb{R}_{+}$](gifs/ab.gif) is a continuous
function and
is a continuous
function and
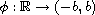 is an increasing homeomorphism
with
is an increasing homeomorphism
with
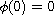 .
We obtain existence, localization and multiplicity
results of positive solutions using Krasnosel'skii fixed point
theorem in cones, and a weak Harnack type inequality. Concerning systems,
the localization is established by the vector version of
Krasnosel'skii theorem, where the compression-expansion conditions
are expressed on components.
.
We obtain existence, localization and multiplicity
results of positive solutions using Krasnosel'skii fixed point
theorem in cones, and a weak Harnack type inequality. Concerning systems,
the localization is established by the vector version of
Krasnosel'skii theorem, where the compression-expansion conditions
are expressed on components.
Submitted February 3, 2016. Published February 18, 2016.
Math Subject Classifications: 34B18, 47H10.
Key Words: Positive solution; phi-Laplacian, boundary value problem;
Krasnosel'skii fixed point theorem; weak Harnack inequality.
An addendum was posted on May 19, 2016. It gives an additional hypothesis
for Theorem 2.2, and gives examples for Theorems 2.4 and 2.5.
See the last four pages of this article.
Show me the PDF file (207 KB),
TEX file for this article.
 |
Diana-Raluca Herlea
Babes-Bolyai University
Department of Mathematics
400084 Cluj, Romania
email: dherlea@math.ubbcluj.ro
|
|---|
Return to the EJDE web page
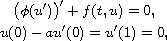
![$f:[0,1]\times \mathbb{R}_{+}\to \mathbb{R}_{+}$](gifs/ab.gif) is a continuous
function and
is a continuous
function and
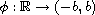 is an increasing homeomorphism
with
is an increasing homeomorphism
with
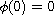 .
We obtain existence, localization and multiplicity
results of positive solutions using Krasnosel'skii fixed point
theorem in cones, and a weak Harnack type inequality. Concerning systems,
the localization is established by the vector version of
Krasnosel'skii theorem, where the compression-expansion conditions
are expressed on components.
.
We obtain existence, localization and multiplicity
results of positive solutions using Krasnosel'skii fixed point
theorem in cones, and a weak Harnack type inequality. Concerning systems,
the localization is established by the vector version of
Krasnosel'skii theorem, where the compression-expansion conditions
are expressed on components.
