Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 45, pp. 1-5.
Non-extinction of solutions to a fast diffusion system
with nonlocal sources
Haixia Li, Yuzhu Han
Abstract:
In this short article, we give a positive answer to the problem
proposed by Zheng et al [5], and show that the fast diffusion
system

under homogeneous Dirichlet boundary condition admits at least one
non-extinction solution when
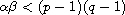 and the initial data are strictly positive.
and the initial data are strictly positive.
Submitted October 28, 2015. Published February 10, 2016.
Math Subject Classifications: 35K40, 35K51.
Key Words: Fast diffusion system; nonlocal source; non-extinction.
Show me the PDF file (185 KB),
TEX file for this article.
 |
Haixia Li
School of Mathematics
Changchun Normal University
Changchun 130032, China
email: lihaixia0611@126.com
|
|---|
 |
Yuzhu Han
School of Mathematics
Jilin University
Changchun 130012, China
email: yzhan@jlu.edu.cn
|
|---|
Return to the EJDE web page

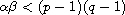 and the initial data are strictly positive.
and the initial data are strictly positive.

