Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 40, pp. 1-13.
Existence of solutions to fractional Hamiltonian systems with
combined nonlinearities
Ziheng Zhang, Rong Yuan
Abstract:
This article concerns the existence of solutions for the
fractional Hamiltonian system

where
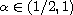 ,
,
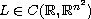 is a symmetric and positive definite matrix.
The novelty of this article is that if
is a symmetric and positive definite matrix.
The novelty of this article is that if
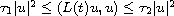 and the nonlinearity
and the nonlinearity
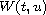 involves a combination of superquadratic
and subquadratic terms, the Hamiltonian system possesses at least two
nontrivial solutions.
involves a combination of superquadratic
and subquadratic terms, the Hamiltonian system possesses at least two
nontrivial solutions.
Submitted November 11, 2015. Published January 27, 2016.
Math Subject Classifications: 34C37, 35A15, 35B38.
Key Words: Fractional Hamiltonian systems; critical point;
variational methods; mountain pass theorem.
Show me the PDF file (269 KB),
TEX file for this article.
 |
Ziheng Zhang
Department of Mathematics
Tianjin Polytechnic University
Tianjin 300387, China
email: zhzh@mail.bnu.edu.cn
|
|---|
 |
Rong Yuan
Department of Mathematical Sciences
Beijing Normal University
Beijing 100875, China
email: ryuan@bnu.edu.cn
|
|---|
Return to the EJDE web page

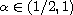 ,
,
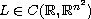 is a symmetric and positive definite matrix.
The novelty of this article is that if
is a symmetric and positive definite matrix.
The novelty of this article is that if
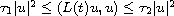 and the nonlinearity
and the nonlinearity
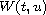 involves a combination of superquadratic
and subquadratic terms, the Hamiltonian system possesses at least two
nontrivial solutions.
involves a combination of superquadratic
and subquadratic terms, the Hamiltonian system possesses at least two
nontrivial solutions.

