Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 35, pp. 1-22.
Existence of two positive solutions for indefinite Kirchhoff equations
in R^3
Ling Ding, Yi-Jie Meng, Shi-Wu Xiao, Jin-Ling Zhang
Abstract:
In this article we study the Kirchhoff type equation
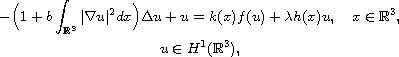
involving a linear part
 which is coercive
if
which is coercive
if
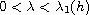 and is noncoercive if
and is noncoercive if
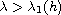 ,
a nonlocal nonlinear term
,
a nonlocal nonlinear term
 and a sign-changing nonlinearity of the form
and a sign-changing nonlinearity of the form
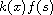 , where
, where
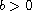 ,
,
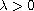 is a real parameter and
is a real parameter and
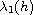 is the first eigenvalue
of
is the first eigenvalue
of
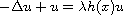 . Under suitable assumptions on
f and h, we obtain positives solution for
. Under suitable assumptions on
f and h, we obtain positives solution for
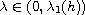 and two positive solutions with a condition on k.
and two positive solutions with a condition on k.
Submitted August 20, 2015. Published January 25, 2016.
Math Subject Classifications: 35J60, 35B38, 35A15.
Key Words: Indefinite Kirchhoff equation; concentration compactness lemma;
(PS) condition; Ekeland's variational principle.
Show me the PDF file (324 KB),
TEX file for this article.
 |
Ling Ding
School of Mathematics and Computer Science
Hubei University of Arts and Science
Hubei 441053, China
email: dingling1975@qq.com, dingling19750118@163.com
|
|---|
 |
Yi-Jie Meng
School of Mathematics and Computer Science
Hubei University of Arts and Science
Hubei 441053, China
email: 245330581@qq.com
|
|---|
 |
Shi-Wu Xiao
School of Mathematics and Computer Science
Hubei University of Arts and Science
Hubei 441053, China
email: xshiwu@sina.com
|
|---|
 |
Jin-Ling Zhang
School of Mathematics and Computer Science
Hubei University of Arts and Science
Hubei 441053, China
email: jinling48@163.com
|
|---|
Return to the EJDE web page
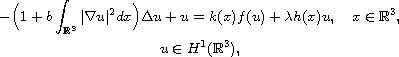
 which is coercive
if
which is coercive
if
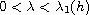 and is noncoercive if
and is noncoercive if
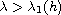 ,
a nonlocal nonlinear term
,
a nonlocal nonlinear term
 and a sign-changing nonlinearity of the form
and a sign-changing nonlinearity of the form
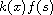 , where
, where
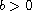 ,
,
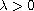 is a real parameter and
is a real parameter and
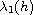 is the first eigenvalue
of
is the first eigenvalue
of
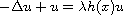 . Under suitable assumptions on
f and h, we obtain positives solution for
. Under suitable assumptions on
f and h, we obtain positives solution for
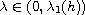 and two positive solutions with a condition on k.
and two positive solutions with a condition on k.



