Electron. J. Differential Equations,
Vol. 2016 (2016), No. 339, pp. 1-18.
Infinitely many solutions for Schrodinger-Kirchhoff type equations
involving the fractional p-Laplacian and critical exponent
Li Wang, Binlin Zhang
Abstract:
In this article, we show the existence of infinitely many solutions for the
fractional p-Laplacian equations of Schrodinger-Kirchhoff type equation
![$$
M([u]_{s, p}^p) (-\Delta )_p^s u+V(x)|u|^{p-2}u=
\alpha |u|^{ p_s^{*}-2 }u+\beta k(x)|u|^{q-2}u \quad x\in \mathbb{R}^N,
$$](gifs/aa.gif)
where
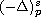 is the fractional p-Laplacian operator,
is the fractional p-Laplacian operator,
![$[u]_{s,p}$](gifs/ac.gif) is the Gagliardo p-seminorm,
is the Gagliardo p-seminorm,
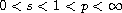 ,
,
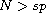 ,
,
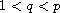 ,
M is a continuous and positive function, V is a continuous
and positive potential function and k(x) is a non-negative function in
an appropriate Lebesgue space. By means of the concentration-compactness
principle in fractional Sobolev space and Kajikiya's new version of the
symmetric mountain pass lemma, we obtain the existence of infinitely many
solutions which tend to zero for suitable positive parameters
,
M is a continuous and positive function, V is a continuous
and positive potential function and k(x) is a non-negative function in
an appropriate Lebesgue space. By means of the concentration-compactness
principle in fractional Sobolev space and Kajikiya's new version of the
symmetric mountain pass lemma, we obtain the existence of infinitely many
solutions which tend to zero for suitable positive parameters
 and
and
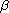 .
.
Submitted October 11, 2016. Published December 30, 2016.
Math Subject Classifications: 35R11, 35A15, 47G20.
Key Words: Schrodinger-Kirchhoff type equation; fractional p-Laplacian;
critical Sobolev exponent.
Show me the PDF file (308 KB),
TEX file for this article.
 |
Li Wang
School of Basic Science
East China Jiaotong University
Nanchang 330013, China
email: wangli.423@163.com
|
|---|
 |
Binlin Zhang
Department of Mathematics
Heilongjiang Institute of Technology
Harbin 150050, China
email: zhangbinlin2012@163.com
|
|---|
Return to the EJDE web page
![$$
M([u]_{s, p}^p) (-\Delta )_p^s u+V(x)|u|^{p-2}u=
\alpha |u|^{ p_s^{*}-2 }u+\beta k(x)|u|^{q-2}u \quad x\in \mathbb{R}^N,
$$](gifs/aa.gif)
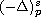 is the fractional p-Laplacian operator,
is the fractional p-Laplacian operator,
![$[u]_{s,p}$](gifs/ac.gif) is the Gagliardo p-seminorm,
is the Gagliardo p-seminorm,
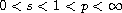 ,
,
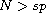 ,
,
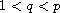 ,
M is a continuous and positive function, V is a continuous
and positive potential function and k(x) is a non-negative function in
an appropriate Lebesgue space. By means of the concentration-compactness
principle in fractional Sobolev space and Kajikiya's new version of the
symmetric mountain pass lemma, we obtain the existence of infinitely many
solutions which tend to zero for suitable positive parameters
,
M is a continuous and positive function, V is a continuous
and positive potential function and k(x) is a non-negative function in
an appropriate Lebesgue space. By means of the concentration-compactness
principle in fractional Sobolev space and Kajikiya's new version of the
symmetric mountain pass lemma, we obtain the existence of infinitely many
solutions which tend to zero for suitable positive parameters
 and
and
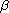 .
.

