Electron. J. Differential Equations,
Vol. 2016 (2016), No. 328, pp. 1-22.
Regularly varying solutions with intermediate growth for cyclic
differential systems of second order
Jaroslav Jaros, Kusano Takasi, Tomoyuki Tanigawa
Abstract:
In this article, we study the existence and accurate asymptotic
behavior as
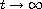 of positive solutions with
intermediate growth for a class of cyclic systems of nonlinear
differential equations of the second order
of positive solutions with
intermediate growth for a class of cyclic systems of nonlinear
differential equations of the second order

where
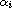 and
and
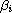 ,
,
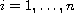 ,
are positive
constants such that
,
are positive
constants such that
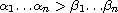 and
and
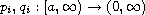 are continuous regularly varying
functions (in the sense of Karamata). It is shown that the situation
in which the system possesses regularly varying intermediate solutions can be
completely characterized, and moreover that the asymptotic
behavior of such solutions is governed by the unique formula
describing their order of growth (or decay) precisely.
The main results are applied to some classes of partial differential
equations with radial symmetry including metaharmonic equations and
systems involving
are continuous regularly varying
functions (in the sense of Karamata). It is shown that the situation
in which the system possesses regularly varying intermediate solutions can be
completely characterized, and moreover that the asymptotic
behavior of such solutions is governed by the unique formula
describing their order of growth (or decay) precisely.
The main results are applied to some classes of partial differential
equations with radial symmetry including metaharmonic equations and
systems involving
 -Laplace
operators on exterior domains.
-Laplace
operators on exterior domains.
Submitted December 30, 2015. Published December 22, 2016.
Math Subject Classifications: 34C11, 26A12.
Key Words: Systems of differential equations; positive solutions;
asymptotic behavior; regularly varying functions.
Show me the PDF file (347 KB),
TEX file for this article.
 |
Jaroslav Jaros
Department of Mathematical Analysis and Numerical Mathematics
Faculty of Mathematics, Physics and Informatics
Comenius University
842 48 Bratislava, Slovakia
email: jaros@fmph.uniba.sk
|
|---|
| |
Kusano Takasi
Department of Mathematics
Faculty of Science,
Hiroshima University
Higashi Hiroshima 739-8526, Japan
email: kusanot@zj8.so-net.ne.jp
|
|---|
| |
Tomoyuki Tanigawa
Department of Mathematics
Faculty of Education,
Kumamoto University
Kumamoto 860-8555, Japan
email: tanigawa@educ.kumamoto-u.ac.jp
|
|---|
Return to the EJDE web page
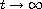 of positive solutions with
intermediate growth for a class of cyclic systems of nonlinear
differential equations of the second order
of positive solutions with
intermediate growth for a class of cyclic systems of nonlinear
differential equations of the second order

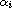 and
and
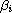 ,
,
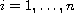 ,
are positive
constants such that
,
are positive
constants such that
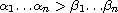 and
and
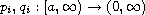 are continuous regularly varying
functions (in the sense of Karamata). It is shown that the situation
in which the system possesses regularly varying intermediate solutions can be
completely characterized, and moreover that the asymptotic
behavior of such solutions is governed by the unique formula
describing their order of growth (or decay) precisely.
The main results are applied to some classes of partial differential
equations with radial symmetry including metaharmonic equations and
systems involving
are continuous regularly varying
functions (in the sense of Karamata). It is shown that the situation
in which the system possesses regularly varying intermediate solutions can be
completely characterized, and moreover that the asymptotic
behavior of such solutions is governed by the unique formula
describing their order of growth (or decay) precisely.
The main results are applied to some classes of partial differential
equations with radial symmetry including metaharmonic equations and
systems involving
 -Laplace
operators on exterior domains.
-Laplace
operators on exterior domains.
