Electron. J. Differential Equations,
Vol. 2016 (2016), No. 327, pp. 1-12.
Nonlinear parabolic equations with blowing-up coefficients
with respect to the unknown and with soft measure data
Khaled Zaki, Hicham Redwane
Abstract:
We establish the existence of solutions for the nonlinear parabolic problem
with Dirichlet homogeneous boundary conditions,
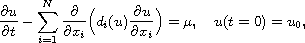
in a bounded domain. The coefficients
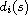 are continuous on an
interval
are continuous on an
interval
![$]-\infty,m[$](gifs/ac.gif) ,
there exists an index p such that
,
there exists an index p such that
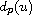 blows up at a finite value m of the unknown u, and
blows up at a finite value m of the unknown u, and
 is a diffuse
measure.
is a diffuse
measure.
Submitted September 9, 2016. Published December 22, 2016.
Math Subject Classifications: 47A15, 46A32, 47D20.
Key Words: Nonlinear parabolic equations; blowing-up coefficients;
renormalized solutions; soft measure.
Show me the PDF file (280 KB),
TEX file for this article.
 |
Khaled Zaki
Faculté des Sciences et Techniques
Université Hassan 1, B.P. 764
Settat, Morocco
email: zakikhaled74@hotmail.com
|
|---|
 |
Hicham Redwane
Faculté des Sciences Juridiques,
Économiques et Sociales
Université Hassan 1, B.P. 764
Settat, Morocco
email: redwane_hicham@yahoo.fr
|
|---|
Return to the EJDE web page
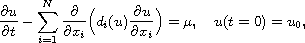
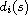 are continuous on an
interval
are continuous on an
interval
![$]-\infty,m[$](gifs/ac.gif) ,
there exists an index p such that
,
there exists an index p such that
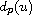 blows up at a finite value m of the unknown u, and
blows up at a finite value m of the unknown u, and
 is a diffuse
measure.
is a diffuse
measure.

