Electron. J. Differential Equations,
Vol. 2016 (2016), No. 325, pp. 1-18.
Existence of solutions for a scalar conservation law with a flux
of low regularity
Martin Lazar, Darko Mitrovic
Abstract:
We prove existence of solutions to Cauchy problem for scalar conservation
laws with non-degenerate discontinuous flux
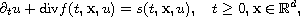
where for every
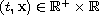 ,
the flux
,
the flux
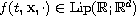 and
and
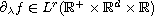 ,
additionally satisfying
,
additionally satisfying
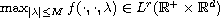 ,
for some
,
for some
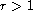 and every
and every
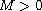 ,
and, for every
,
and, for every
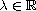 ,
,
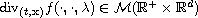 where
where
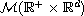 is the space of Radon measures.
Moreover, the function s is measurable and both f and s satisfy certain
growth rate assumptions with respect to
is the space of Radon measures.
Moreover, the function s is measurable and both f and s satisfy certain
growth rate assumptions with respect to
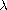 .
The result is obtained
by means of the H-measures.
.
The result is obtained
by means of the H-measures.
Submitted May 18, 2016. Published December 22, 2016.
Math Subject Classifications: 35L65.
Key Words: Scalar conservation law; discontinuous coefficient; existence;
velocity averaging; H-measure.
Show me the PDF file (346 KB),
TEX file for this article.
 |
Martin Lazar
University of Dubrovnik, Croatia
email: mlazar@unidu.hr
|
|---|
 |
Darko Mitrović
Faculty of Mathematics
University of Montenegro
Montenegro
email: darkom@ac.me
|
|---|
Return to the EJDE web page
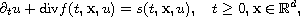
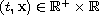 ,
the flux
,
the flux
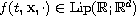 and
and
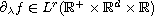 ,
additionally satisfying
,
additionally satisfying
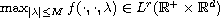 ,
for some
,
for some
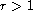 and every
and every
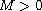 ,
and, for every
,
and, for every
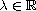 ,
,
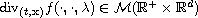 where
where
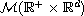 is the space of Radon measures.
Moreover, the function s is measurable and both f and s satisfy certain
growth rate assumptions with respect to
is the space of Radon measures.
Moreover, the function s is measurable and both f and s satisfy certain
growth rate assumptions with respect to
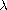 .
The result is obtained
by means of the H-measures.
.
The result is obtained
by means of the H-measures.

