Electron. J. Differential Equations,
Vol. 2016 (2016), No. 318, pp. 1-22.
Upper bounds for the number of limit cycles of polynomial differential system
Selma Ellaggoune, Sabrina Badi
Abstract:
For
 small we consider the number of
limit cycles of the polynomial differential system
small we consider the number of
limit cycles of the polynomial differential system
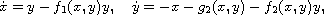
where
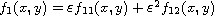 ,
,
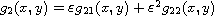 and
and
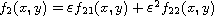 where
where
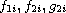 have degree
have degree
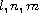 respectively for each
respectively for each
 .
We provide an accurate upper bound of the maximum number of limit cycles that
this class of systems can have bifurcating from the periodic
orbits of the linear center
.
We provide an accurate upper bound of the maximum number of limit cycles that
this class of systems can have bifurcating from the periodic
orbits of the linear center
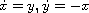 using the
averaging theory of first and second order. We give an example for which
this bound is reached.
using the
averaging theory of first and second order. We give an example for which
this bound is reached.
Submitted October 1, 2016. Published December 14, 2016.
Math Subject Classifications: 34C25, 34C29, 37G15.
Key Words: Limit cycle; Lienard differential equation; averaging method.
Show me the PDF file (238 KB),
TEX file for this article.
 |
Selma Ellaggoune
Laboratory of Applied Mathematics and Modeling
University 8 Mai 1945
Guelma, Algeria
email: sellaggoune@gmail.com
|
|---|
 |
Sabrina Badi
Laboratory of Applied Mathematics and Modeling
University 8 Mai 1945
Guelma, Algeria
email: badisabrina@yahoo.fr
|
|---|
Return to the EJDE web page
 small we consider the number of
limit cycles of the polynomial differential system
small we consider the number of
limit cycles of the polynomial differential system
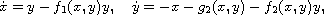
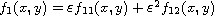 ,
,
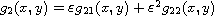 and
and
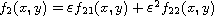 where
where
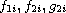 have degree
have degree
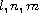 respectively for each
respectively for each
 .
We provide an accurate upper bound of the maximum number of limit cycles that
this class of systems can have bifurcating from the periodic
orbits of the linear center
.
We provide an accurate upper bound of the maximum number of limit cycles that
this class of systems can have bifurcating from the periodic
orbits of the linear center
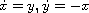 using the
averaging theory of first and second order. We give an example for which
this bound is reached.
using the
averaging theory of first and second order. We give an example for which
this bound is reached.

