Electron. J. Differential Equations,
Vol. 2016 (2016), No. 317, pp. 1-9.
Sign-changing solutions for asymptotically linear Schrodinger equation
in bounded domains
Sitong Chen, Yinbin Li, Xianhua Tang
Abstract:
In this article we study the Schrodinger equation
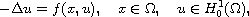
where
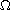 is a bounded domain in
is a bounded domain in
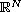 and f(x,u) is
asymptotically linear at infinity with respect to u.
Inspired by the works of Salvatore [14] on sign-changing solutions,
in which
and f(x,u) is
asymptotically linear at infinity with respect to u.
Inspired by the works of Salvatore [14] on sign-changing solutions,
in which
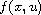 is asymptotically linear at zero with respect to u,
we prove, via the constraint variational method and the quantitative
deformation lemma, that the equation possesses one sign-changing solution
with exactly two nodal domains.
is asymptotically linear at zero with respect to u,
we prove, via the constraint variational method and the quantitative
deformation lemma, that the equation possesses one sign-changing solution
with exactly two nodal domains.
Submitted June 22, 2016. Published December 14, 2016.
Math Subject Classifications: 35J10, 35J20.
Key Words: Schrodinger equation; sign-changing solutions;
asymptotically linear.
Show me the PDF file (229 KB),
TEX file for this article.
 |
Sitong Chen
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: mathsitongchen@163.com
|
|---|
 |
Yinbin Li
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: liyinbin1991@163.com
|
|---|
 |
Xianhua Tang
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: tangxh@mail.csu.edu.cn
|
|---|
Return to the EJDE web page
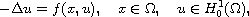
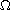 is a bounded domain in
is a bounded domain in
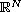 and f(x,u) is
asymptotically linear at infinity with respect to u.
Inspired by the works of Salvatore [14] on sign-changing solutions,
in which
and f(x,u) is
asymptotically linear at infinity with respect to u.
Inspired by the works of Salvatore [14] on sign-changing solutions,
in which
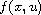 is asymptotically linear at zero with respect to u,
we prove, via the constraint variational method and the quantitative
deformation lemma, that the equation possesses one sign-changing solution
with exactly two nodal domains.
is asymptotically linear at zero with respect to u,
we prove, via the constraint variational method and the quantitative
deformation lemma, that the equation possesses one sign-changing solution
with exactly two nodal domains.


