We expand upon the basic oscillation theory for general boundary problems of the form
![$$-y''+q(t)y=\lambda r(t)y, \quad t \in I = [a,b]
$$](gifs/aa.gif)
where q and r are real-valued piecewise continuous functions and y is required to satisfy a pair of homogeneous separated boundary conditions at the end-points. The non-definite case is characterized by the indefiniteness of each of the quadratic forms
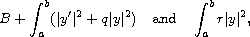
over a suitable space where B is a boundary term. In 1918 Richardson proved that, in the case of the Dirichlet problem, if r(t) changes its sign exactly once and the boundary problem is non-definite then the zeros of the real and imaginary parts of any non-real eigenfunction interlace. We show that, unfortunately, this result is false in the case of two turning points, thus removing any hope for a general separation theorem for the zeros of the non-real eigenfunctions. Furthermore, we show that when a non-real eigenfunction vanishes inside I, the absolute value of the difference between the total number of zeros of its real and imaginary parts is exactly 2.

