Electron. J. Differential Equations,
Vol. 2016 (2016), No. 306, pp. 1-11.
Multiplicity of solutions to a nonlocal Choquard equation
involving fractional magnetic operators and critical exponent
Fuliang Wang, Mingqi Xiang
Abstract:
In this article, we study the multiplicity of solutions to a nonlocal
fractional Choquard equation involving an external magnetic potential
and critical exponent, namely,
![$$\displaylines{
(a+b[u]_{s,A}^2)(-\Delta)_A^su+V(x)u
=\int_{\mathbb{R}^N}\frac{|u(y)|^{2_{\mu,s}^*}}{|x-y|^{\mu}}dy|u|^{2_{\mu,s}^*-2}u
+\lambda h(x)|u|^{p-2}u\quad \text{in }\mathbb{R}^N,
\cr
[u]_{s,A}=\Big(\int_{\mathbb{R}^{N}}\int_{\mathbb{R}^N}
\frac{|u(x)-e^{i(x-y)\cdot A(\frac{x+y}{2})}u(y)|^2}{|x-y|^{N+2s}}\,dx\,dy\Big)
^{1/2}
}$$](gifs/aa.gif)
where
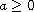 , b>0,
, b>0,
 ,
,
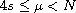 ,
,
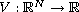 is a sign-changing scalar potential,
is a sign-changing scalar potential,
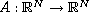 is the magnetic potential,
is the magnetic potential,
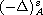 is the fractional magnetic operator,
is the fractional magnetic operator,
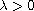 is a parameter,
is a parameter,
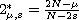 is the critical exponent
in the sense of the Hardy-Littlewood-Sobolev inequality and
is the critical exponent
in the sense of the Hardy-Littlewood-Sobolev inequality and
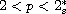 .
Under suitable assumptions on a,b and
.
Under suitable assumptions on a,b and
 ,
we obtain multiplicity
of nontrivial solutions by using variational methods.
In particular, we obtain the existence of infinitely many nontrivial solutions
for the degenerate Kirchhoff case, that is, a=0, b>0.
,
we obtain multiplicity
of nontrivial solutions by using variational methods.
In particular, we obtain the existence of infinitely many nontrivial solutions
for the degenerate Kirchhoff case, that is, a=0, b>0.
Submitted October 27, 2016. Published November 30, 2016.
Math Subject Classifications: 49A50, 26A33, 35J60, 47G20.
Key Words: Choquard equation; fractional magnetic operator;
variational method; critical exponent.
Show me the PDF file (277 KB),
TEX file for this article.
 |
Fuliang Wang
College of Science
Civil Aviation University of China
Tianjin 300300, China
email: flwang@cauc.edu.cn
|
|---|
 |
Mingqi Xiang
College of Science
Civil Aviation University of China
Tianjin 300300, China
email: xiangmingqi_hit@163.com
|
|---|
Return to the EJDE web page
![$$\displaylines{
(a+b[u]_{s,A}^2)(-\Delta)_A^su+V(x)u
=\int_{\mathbb{R}^N}\frac{|u(y)|^{2_{\mu,s}^*}}{|x-y|^{\mu}}dy|u|^{2_{\mu,s}^*-2}u
+\lambda h(x)|u|^{p-2}u\quad \text{in }\mathbb{R}^N,
\cr
[u]_{s,A}=\Big(\int_{\mathbb{R}^{N}}\int_{\mathbb{R}^N}
\frac{|u(x)-e^{i(x-y)\cdot A(\frac{x+y}{2})}u(y)|^2}{|x-y|^{N+2s}}\,dx\,dy\Big)
^{1/2}
}$$](gifs/aa.gif)
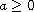 , b>0,
, b>0,
 ,
,
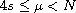 ,
,
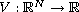 is a sign-changing scalar potential,
is a sign-changing scalar potential,
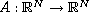 is the magnetic potential,
is the magnetic potential,
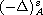 is the fractional magnetic operator,
is the fractional magnetic operator,
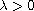 is a parameter,
is a parameter,
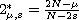 is the critical exponent
in the sense of the Hardy-Littlewood-Sobolev inequality and
is the critical exponent
in the sense of the Hardy-Littlewood-Sobolev inequality and
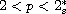 .
Under suitable assumptions on a,b and
.
Under suitable assumptions on a,b and
 ,
we obtain multiplicity
of nontrivial solutions by using variational methods.
In particular, we obtain the existence of infinitely many nontrivial solutions
for the degenerate Kirchhoff case, that is, a=0, b>0.
,
we obtain multiplicity
of nontrivial solutions by using variational methods.
In particular, we obtain the existence of infinitely many nontrivial solutions
for the degenerate Kirchhoff case, that is, a=0, b>0.

