Electron. J. Differential Equations,
Vol. 2016 (2016), No. 302, pp. 1-16.
Asymptotic stability of non-autonomous functional
differential equations with distributed delays
Laszlo Hatvani
Abstract:
We consider the integro differential equation

where
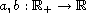 ,
,
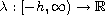 are piecewise continuous functions and
are piecewise continuous functions and
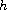 is a positive constant.
We establish sufficient conditions guaranteeing either asymptotic stability
or uniform asymptotic stability for the zero solution. These conditions
state that the instantaneous stabilizing term on the right-hand side dominates
in some sense the perturbation term with delays.
Our conditions not require
is a positive constant.
We establish sufficient conditions guaranteeing either asymptotic stability
or uniform asymptotic stability for the zero solution. These conditions
state that the instantaneous stabilizing term on the right-hand side dominates
in some sense the perturbation term with delays.
Our conditions not require
 being bounded from above. The results are
based on the method of Lyapunov functionals and Razumikhin functions.
being bounded from above. The results are
based on the method of Lyapunov functionals and Razumikhin functions.
Submitted October 5, 2016. Published November 25, 2016.
Math Subject Classifications: 34K20, 34K27, 34D20.
Key Words: Annulus argument; uniform asymptotic stability.
Show me the PDF file (289 KB),
TEX file for this article.
 |
László Hatvani
University of Szeged, Bolyai Institute
Aradi vértanúk tere 1
H-6720 Szeged, Hungary
email: hatvani@math.u-szeged.hu
|
|---|
Return to the EJDE web page

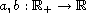 ,
,
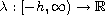 are piecewise continuous functions and
are piecewise continuous functions and
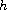 is a positive constant.
We establish sufficient conditions guaranteeing either asymptotic stability
or uniform asymptotic stability for the zero solution. These conditions
state that the instantaneous stabilizing term on the right-hand side dominates
in some sense the perturbation term with delays.
Our conditions not require
is a positive constant.
We establish sufficient conditions guaranteeing either asymptotic stability
or uniform asymptotic stability for the zero solution. These conditions
state that the instantaneous stabilizing term on the right-hand side dominates
in some sense the perturbation term with delays.
Our conditions not require
 being bounded from above. The results are
based on the method of Lyapunov functionals and Razumikhin functions.
being bounded from above. The results are
based on the method of Lyapunov functionals and Razumikhin functions.
