Electron. J. Differential Equations,
Vol. 2016 (2016), No. 287, pp. 1-14.
Gap solitons in periodic Schrödinger lattice
system with nonlinear hopping
Ming Cheng, Alexander Pankov
Abstract:
This article concerns the periodic discrete Schrödinger equation with
nonlinear hopping on the infinite integer lattice. We obtain the
existence of gap solitons by the linking theorem and concentration compactness
method together with a periodic approximation technique.
In addition, the behavior of such solutions is studied as
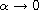 .
Notice that the nonlinear hopping can be sign changing.
.
Notice that the nonlinear hopping can be sign changing.
Submitted October 7, 2016. Published October 26, 2016.
Math Subject Classifications: 35Q55, 35Q51, 39A12, 39A70, 78A40.
Key Words: Discrete nonlinear Schrödinger equation; nonlinear hopping;
gap soliton; linking theorem; periodic approximation.
Show me the PDF file (242 KB),
TEX file for this article.
 |
Ming Cheng
College of Mathematics
Jilin University
Changchun 130012, China
email: jlumcheng@hotmail.com
|
|---|
 |
Alexander Pankov
Department of Mathematics
Morgan State University
Baltimore, MD 21251, USA
email: alexander.pankov@morgan.edu
|
|---|
Return to the EJDE web page
 .
Notice that the nonlinear hopping can be sign changing.
.
Notice that the nonlinear hopping can be sign changing.

