Electron. J. Differential Equations,
Vol. 2016 (2016), No. 276, pp. 1-8.
Multiple solutions for Schr\"odinger-Poisson systems with sign-changing
potential and critical nonlinearity
Liuyang Shao, Haibo Chen
Abstract:
In this article, we study the Schr\"odinger-Poisson system
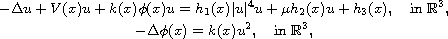
where
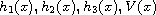 are allowed to be sign-changing
and
are allowed to be sign-changing
and
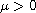 is a parameter. Under some appropriate assumptions on V(x),
we obtain the existence of two different solutions for the above system
via variational methods.
is a parameter. Under some appropriate assumptions on V(x),
we obtain the existence of two different solutions for the above system
via variational methods.
Submitted March 12, 2016. Published October 17, 2016.
Math Subject Classifications: 35B38, 35G99.
Key Words: Schrodinger-Poisson system; variational methods;
mountain pass theorem; Ekeland's variational principle.
Show me the PDF file (213 KB),
TEX file for this article.
 |
Liuyang Shao
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: sliuyang316@163.com
|
|---|
 |
Haibo Chen
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: math_chb@163.com
|
|---|
Return to the EJDE web page
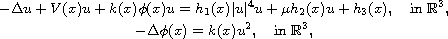
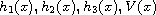 are allowed to be sign-changing
and
are allowed to be sign-changing
and
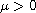 is a parameter. Under some appropriate assumptions on V(x),
we obtain the existence of two different solutions for the above system
via variational methods.
is a parameter. Under some appropriate assumptions on V(x),
we obtain the existence of two different solutions for the above system
via variational methods.

