Electron. J. Differential Equations,
Vol. 2016 (2016), No. 273, pp. 1-8.
Solvability of singular second-order initial-value problems
Petio Kelevedjiev
Abstract:
This article concerns the solvability of the initial-value problem
x''=f(t,x,x'), x(0)=A, x'(0)=B, where the scalar function f
may be unbounded as
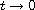 . Using barrier strip type arguments,
we establish the existence of monotone and/or positive solutions
in
. Using barrier strip type arguments,
we establish the existence of monotone and/or positive solutions
in
![$C^1[0,T]\cap C^2(0,T]$](gifs/ab.gif) .
.
Submitted April 8, 2016. Published October 12, 2016.
Math Subject Classifications: 34A12, 34A36.
Key Words: Initial value problem; second order differential equation;
singularity; existence; barrier conditions.
Show me the PDF file (194 KB),
TEX file for this article.
 |
Petio Kelevedjiev
Technical University of Sofia
Branch Sliven, Bulgaria
email: keleved@mailcity.com
|
|---|
Return to the EJDE web page
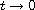 . Using barrier strip type arguments,
we establish the existence of monotone and/or positive solutions
in
. Using barrier strip type arguments,
we establish the existence of monotone and/or positive solutions
in
![$C^1[0,T]\cap C^2(0,T]$](gifs/ab.gif) .
.
