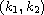Electron. J. Differential Equations, Vol. 2016 (2016), No. 272, pp. 1-8.

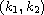Existence of positive entire radial solutions to a $(k_1,k_2)$-Hessian systems with convection terms

Dragos-Patru Covei

Abstract:
In this article, we prove two new results on the existence of positive entire large and bounded radial solutions for nonlinear system with gradient terms
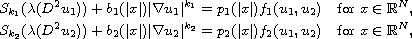
$$\displaylines{ S_{k_1}(\lambda (D^{2}u_1) )+b_1(| x| ) | \nabla u_1|^{k_1} =p_1(| x| ) f_1(u_1,u_2) \quad\text{for }x\in \mathbb{R}^{N}, \cr S_{k_2}(\lambda (D^{2}u_2) ) +b_2(| x| ) | \nabla u_2|^{k_2} =p_2(| x| ) f_2(u_1,u_2) \quad\text{for }x\in \mathbb{R}^{N}, }$$
where 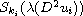$S_{k_i}(\lambda (D^{2}u_i) ) $ is the 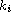$k_i$-Hessian operator, 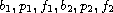$b_1,p_1, f_1, b_2, p_2,f_2$ are continuous functions satisfying certain properties. Our results expand those by Zhang and Zhou [23]. The main difficulty in dealing with our system is the presence of the convection term.

Submitted August 23, 2016. Published October 10, 2016.
Math Subject Classifications: 35J25, 35J47, 35J96.
Key Words: Entire solution; large solution; elliptic system.

Show me the PDF file (218 KB), TEX file for this article.

Dragos-Patru Covei
Department of Applied Mathematics
The Bucharest University of Economic Studies
Piata Romana, 1st district, postal code 010374
postal office 22, Romania
email: coveidragos@yahoo.com}

Return to the EJDE web page