Electron. J. Differential Equations,
Vol. 2016 (2016), No. 270, pp. 1-12.
Weighted pseudo almost automorphic and S-asymptotically
omega-periodic solutions to fractional difference-differential equations
Edgardo Alvarez, Carlos Lizama
Abstract:
We study weighted pseudo almost automorphic solutions for the nonlinear
fractional difference equation
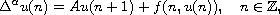
for
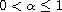 ,
where A is the generator of an
,
where A is the generator of an
 -resolvent
sequence
-resolvent
sequence
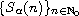 in
in
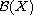 .
We prove the existence and uniqueness of a weighted pseudo almost automorphic
solution assuming that f(.,.) is weighted almost automorphic
in the first variable and satisfies a Lipschitz (local and global)
type condition in the second variable. An analogous result is also proved
for
.
We prove the existence and uniqueness of a weighted pseudo almost automorphic
solution assuming that f(.,.) is weighted almost automorphic
in the first variable and satisfies a Lipschitz (local and global)
type condition in the second variable. An analogous result is also proved
for
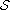 -asymptotically
-asymptotically
 -periodic solutions.
-periodic solutions.
Submitted July 5, 2016. Published October 7, 2016.
Math Subject Classifications: 32N05, 65Q10, 47B39.
Key Words: Weyl-like fractional difference; fractional difference equation;
weighted pseudo almost automorphic sequence;
alpha-resolvent sequences of operators
Show me the PDF file (250 KB),
TEX file for this article.
 |
Edgardo Alvarez
Universidad del Norte
Departamento de Matemáticas y Estadística
Barranquilla, Colombia
email: ealvareze@uninorte.edu.co
|
|---|
 |
Carlos Lizama
Universidad de Santiago de Chile
Facultad de Ciencia
Departamento de Matemática y Ciencia de la Computacióon
Las Sophoras 173, Estación Central
Santiago, Chile
email: carlos.lizama@usach.cl
|
|---|
Return to the EJDE web page
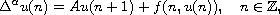
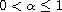 ,
where A is the generator of an
,
where A is the generator of an
 -resolvent
sequence
-resolvent
sequence
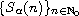 in
in
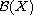 .
We prove the existence and uniqueness of a weighted pseudo almost automorphic
solution assuming that f(.,.) is weighted almost automorphic
in the first variable and satisfies a Lipschitz (local and global)
type condition in the second variable. An analogous result is also proved
for
.
We prove the existence and uniqueness of a weighted pseudo almost automorphic
solution assuming that f(.,.) is weighted almost automorphic
in the first variable and satisfies a Lipschitz (local and global)
type condition in the second variable. An analogous result is also proved
for
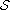 -asymptotically
-asymptotically
 -periodic solutions.
-periodic solutions.

