In this article, we study a density-dependent predator-prey system with the Beddington-DeAngelis functional response for stability and Hopf bifurcation under certain parametric conditions. We start with the condition of the existence of the unique positive equilibrium, and provide two sufficient conditions for its local stability by the Lyapunov function method and the Routh-Hurwitz criterion, respectively. Then, we establish sufficient conditions for the global stability of the positive equilibrium by proving the non-existence of closed orbits in the first quadrant
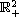 .
Afterwards, we analyze the Hopf bifurcation geometrically by
exploring the monotonic property of the trace of the Jacobean matrix with
respect to
.
Afterwards, we analyze the Hopf bifurcation geometrically by
exploring the monotonic property of the trace of the Jacobean matrix with
respect to
 and analytically verifying that there is a unique
and analytically verifying that there is a unique
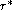 such that the trace is equal to 0.
We also introduce an auxiliary map by restricting all the five parameters
to a special one-dimensional geometrical structure and analyze the Hopf
bifurcation with respect to all these five parameters. Finally, some
numerical simulations are illustrated which are in agreement with our
analytical results.
such that the trace is equal to 0.
We also introduce an auxiliary map by restricting all the five parameters
to a special one-dimensional geometrical structure and analyze the Hopf
bifurcation with respect to all these five parameters. Finally, some
numerical simulations are illustrated which are in agreement with our
analytical results.


