Flavio Roberto Dias Silva, Joao Manoel Soriano Pitot, Andre Vicente
Abstract:
We discuss the global well-posedness and uniform exponential stability
for the Kirchhoff equation in
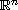
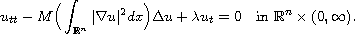
The global solvability is proved when the initial data are taken small
enough and the exponential decay of the energy is obtained in the strong
topology
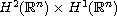 , which is a different
feature of the present article when compared with the prior literature.
We also dedicate a section to discuss a model with the frictional damping term
, which is a different
feature of the present article when compared with the prior literature.
We also dedicate a section to discuss a model with the frictional damping term
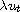 ,
is replaced by a viscoelastic damping term
,
is replaced by a viscoelastic damping term
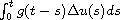 .
.
Submitted June 17, 2016. Published September 12, 2016.
Math Subject Classifications: 35B35, 35B40, 35B45, 35B70.
Key Words: Kirchhoff equation; existence and uniqueness of solution;
uniform stability; exponential decay;
frictional damping; viscoelastic damping.
Show me the PDF file (389 KB), TEX file for this article.
 |
Flávio Roberto Dias Silva Universidade Estadual do Oeste do Paraná - CCET Rua Universitária, 2069, Jd. Universitário CEP: 85819-110, Cascavel, PR, Brazil email: frdsilva@yahoo.com.br |
|---|---|
 |
João Manoel Soriano Pitot Universidade Estadual Paulista Rua Cristóvão Colombo, 2265, Jd. Nazareth CEP: 15054-000, São José do Rio Preto, SP, Brazil email: john.pitot@gmail.com |
 |
André Vicente Universidade Estadual do Oeste do Paraná - CCET Rua Universitária, 2069, Jd. Universitário CEP: 85819-110, Cascavel, PR, Brazil email: andre.vicente@unioeste.br |
Return to the EJDE web page