Electron. J. Differential Equations,
Vol. 2016 (2016), No. 235, pp. 1-13.
Existence and regularity of solutions to the Leray-alpha model
with Navier slip boundary conditions
Hani Ali, Petr Kaplicky
Abstract:
We establish the existence and regularity of a unique weak solution
to turbulent flows in a bounded domain
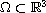 governed by the Leray-alpha model with Navier slip boundary condition
for the velocity. Furthermore, we show that when the filter coefficient
alpha tends to zero, these weak solutions converge to a suitable weak
solution to the incompressible Navier Stokes equations subject to the
Navier boundary conditions. Finally, we discuss the relation between
the Leray-alpha model and the Navier-Stokes
equations with homogeneous Dirichlet boundary condition.
governed by the Leray-alpha model with Navier slip boundary condition
for the velocity. Furthermore, we show that when the filter coefficient
alpha tends to zero, these weak solutions converge to a suitable weak
solution to the incompressible Navier Stokes equations subject to the
Navier boundary conditions. Finally, we discuss the relation between
the Leray-alpha model and the Navier-Stokes
equations with homogeneous Dirichlet boundary condition.
Submitted April 15, 2013. Published August 26, 2016.
Math Subject Classifications: 35Q30, 35Q35, 76F60.
Key Words: Turbulence model; existence of solutions; weak solution.
Show me the PDF file (285 KB),
TEX file for this article.
 |
Hani Ali
AXA Global P & C
Paris, France
email: hani.ali@axa.com
|
|---|
 |
Petr Kaplicky
Charles University
Faculty of Mathematics and Physics
Sokolovska 83
186 75 Prague 8, Czech Republic
email: kaplicky@karlin.mff.cuni.cz
|
|---|
Return to the EJDE web page
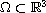 governed by the Leray-alpha model with Navier slip boundary condition
for the velocity. Furthermore, we show that when the filter coefficient
alpha tends to zero, these weak solutions converge to a suitable weak
solution to the incompressible Navier Stokes equations subject to the
Navier boundary conditions. Finally, we discuss the relation between
the Leray-alpha model and the Navier-Stokes
equations with homogeneous Dirichlet boundary condition.
governed by the Leray-alpha model with Navier slip boundary condition
for the velocity. Furthermore, we show that when the filter coefficient
alpha tends to zero, these weak solutions converge to a suitable weak
solution to the incompressible Navier Stokes equations subject to the
Navier boundary conditions. Finally, we discuss the relation between
the Leray-alpha model and the Navier-Stokes
equations with homogeneous Dirichlet boundary condition.

