In this article we study radial solutions of
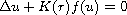 on the exterior of the ball of radius R>0 centered at the origin in
on the exterior of the ball of radius R>0 centered at the origin in
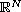 where f is odd with f<0 on
where f is odd with f<0 on
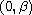 ,
f>0 on
,
f>0 on
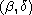 ,
,
 for
for
 ,
and where the function
K(r) is assumed to be positive and
,
and where the function
K(r) is assumed to be positive and
 as
as
 .
The primitive
.
The primitive
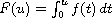 has a "hilltop" at
has a "hilltop" at
 .
We prove that if
.
We prove that if
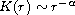 with
with
 and if R>0 is sufficiently small then there are a finite number of
solutions of
and if R>0 is sufficiently small then there are a finite number of
solutions of
 on the exterior of the ball of
radius R such that
on the exterior of the ball of
radius R such that
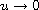 as
as
 .
We also prove the
nonexistence of solutions if R is sufficiently large.
.
We also prove the
nonexistence of solutions if R is sufficiently large.
