In this article, we consider the Kirchhoff equation
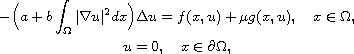
and under suitable assumptions on the main term f in the equation, some existence results are obtained by the variational methods and some analysis techniques.
Yong-Yi Lan
Abstract:
In this article, we consider the Kirchhoff equation
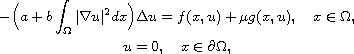
and under suitable assumptions on the main term f
in the equation,
some existence results are obtained by the variational methods and some
analysis techniques.
Submitted February 16, 2016. Published August 18, 2016.
Math Subject Classifications: 35J60, 35J65, 53C35.
Key Words: Kirchhoff equation; Dirichlet boundary condition;
mountain pass theorem; perturbation problem.
Show me the PDF file (259 KB), TEX file for this article.
 |
Yong-Yi Lan School of Mathematical Sciences Xiamen University Xiamen 361005, China email: lanyongyi@jmu.edu.cn |
|---|
Return to the EJDE web page