Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 222, pp. 1-20.
Nonlinear Schrodinger equations on the half-line with nonlinear
boundary conditions
Ahmet Batal, Turker Ozsari
Abstract:
In this article, we study the initial boundary value problem for
nonlinear Schrodinger equations on the half-line with nonlinear
boundary conditions
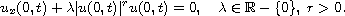
We discuss the local well-posedness when the initial data
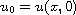 belongs to an
belongs to an
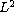 -based
inhomogeneous Sobolev space
-based
inhomogeneous Sobolev space
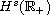 with
with
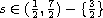 .
We deal with the nonlinear boundary condition by first studying the linear
Schrodinger equation with a time-dependent inhomogeneous Neumann boundary
condition
.
We deal with the nonlinear boundary condition by first studying the linear
Schrodinger equation with a time-dependent inhomogeneous Neumann boundary
condition
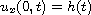 where
where
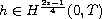 .
.
Submitted March 2, 2016. Published August 17, 2016.
Math Subject Classifications: 35Q55, 35A01, 35A02, 35B30.
Key Words: Nonlinear Schrodinger equations; nonlinear boundary conditions;
local well-posedness; inhomogeneous boundary conditions.
Show me the PDF file (334 KB),
TEX file for this article.
 |
Ahmet Batal
Department of Mathematics
Izmir Institute of Technology
Izmir, Turkey
email: ahmetbatal@iyte.edu.tr
|
|---|
 |
Turker Ozsari
Department of Mathematics
Izmir Institute of Technology
Izmir, Turkey
email: turkerozsari@iyte.edu.tr
|
|---|
Return to the EJDE web page
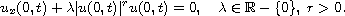
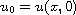 belongs to an
belongs to an
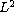 -based
inhomogeneous Sobolev space
-based
inhomogeneous Sobolev space
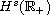 with
with
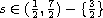 .
We deal with the nonlinear boundary condition by first studying the linear
Schrodinger equation with a time-dependent inhomogeneous Neumann boundary
condition
.
We deal with the nonlinear boundary condition by first studying the linear
Schrodinger equation with a time-dependent inhomogeneous Neumann boundary
condition
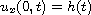 where
where
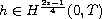 .
.

