In this article we study the fourth-order viscoelastic plate equation
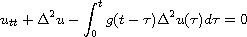
in the bounded domain
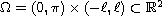 with non traditional boundary conditions. We establish the well-posedness
and a decay result.
with non traditional boundary conditions. We establish the well-posedness
and a decay result.
Salim A. Messaoudi, Soh Edwin Mukiawa
Abstract:
In this article we study the fourth-order viscoelastic plate equation
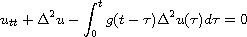
in the bounded domain
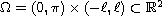 with non traditional boundary conditions. We establish the well-posedness
and a decay result.
with non traditional boundary conditions. We establish the well-posedness
and a decay result.
Submitted October 12, 2015. Published January 13, 2016.
Math Subject Classifications: 35L35, 37B25, 34D20, 74H20, 74H25.
Key Words: Existence; decay; plate viscoelastic; fourth order.
Show me the PDF file (248 KB), TEX file for this article.
 |
Salim A. Messaoudi Department of Mathematics and Statistics King Fahd University of Petroleum and Minerals Dhahran 31261, Saudi Arabia email: messaoud@kfupm.edu.sa |
|---|---|
| Soh Edwin Mukiawa Department of Mathematics and Statistics King Fahd University of Petroleum and Minerals Dhahran 31261, Saudi Arabia email: g201206120@kfupm.edu.sa |
Return to the EJDE web page