Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 218, pp. 1-19.
Existence of solutions to nonlinear fractional
Schrodinger equations with singular potentials
Qingxuan Wang, Dun Zhao, Kai Wang
Abstract:
We study the eigenvalue problem

where
 ,
,
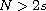 ,
,
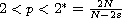 , V(x) is
indefinite and allowed to be unbounded from below, and K(x) is
nonnegative and allowed to be unbounded from above.
When
, V(x) is
indefinite and allowed to be unbounded from below, and K(x) is
nonnegative and allowed to be unbounded from above.
When
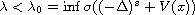 (the lowest spectrum of the operator
(the lowest spectrum of the operator
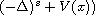 ,
we obtain a positive ground state solution by using the
constrained minimization method. Also we discuss the regularity of
solutions.
,
we obtain a positive ground state solution by using the
constrained minimization method. Also we discuss the regularity of
solutions.
Submitted November 22, 2015. Published August 16, 2016.
Math Subject Classifications: 35R11.
Key Words: Nonlinear fractional Schrodinger equation; ground state;
positive solution; weakly continuous.
Show me the PDF file (317 KB),
TEX file for this article.
 |
Qingxuan Wang
School of Mathematics and Statistics
Lanzhou University
Lanzhou 730000, China
email: wangqx12@lzu.edu.cn
Fax +86 931 8912481
|
|---|
 |
Dun Zhao
School of Mathematics and Statistics
Lanzhou University
Lanzhou 730000, China
email: zhaod@lzu.edu.cn
|
|---|
 |
Kai Wang
School of Mathematics and Statistics
Lanzhou University
Lanzhou 730000, China
email: wangk2010@lzu.edu.cn
|
|---|
Return to the EJDE web page

 ,
,
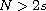 ,
,
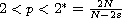 , V(x) is
indefinite and allowed to be unbounded from below, and K(x) is
nonnegative and allowed to be unbounded from above.
When
, V(x) is
indefinite and allowed to be unbounded from below, and K(x) is
nonnegative and allowed to be unbounded from above.
When
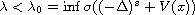 (the lowest spectrum of the operator
(the lowest spectrum of the operator
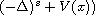 ,
we obtain a positive ground state solution by using the
constrained minimization method. Also we discuss the regularity of
solutions.
,
we obtain a positive ground state solution by using the
constrained minimization method. Also we discuss the regularity of
solutions.


