Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 208, pp. 1-15.
Well-posedness of non-autonomous degenerate parabolic equations
under singular perturbations
Jingyu Wang, Yejuan Wang, Dun Zhao
Abstract:
This article concerns the asymptotic behavior of the following
non-autonomous degenerate parabolic equation with singular perturbations
defined on a bounded domain in
 ,
,
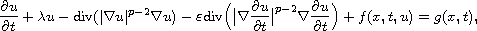
where
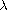 is a positive constant,
is a positive constant,
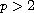 and
and
![$\varepsilon\in(0,1]$](gifs/ae.gif) .
The well-posedness and upper semicontinuity of pullback attractors
are established for the problem without the uniqueness of solutions
under singular perturbations.
.
The well-posedness and upper semicontinuity of pullback attractors
are established for the problem without the uniqueness of solutions
under singular perturbations.
Submitted August 3, 2015. Published August 2, 2016.
Math Subject Classifications: 34K26, 35B41, 35K65.
Key Words: Pullback attractor; multi-valued process; upper semicontinuity;
p-laplacian equation; singular perturbation.
Show me the PDF file (293 KB),
TEX file for this article.
| |
Jingyu Wang
School of Mathematics and Statistics
Gansu Key Laboratory of Applied
Mathematics and Complex Systems
Lanzhou University, Lanzhou 730000, China
email: wangjy418@qq.com
|
|---|
 |
Yejuan Wang
School of Mathematics and Statistics
Gansu Key Laboratory of Applied
Mathematics and Complex Systems
Lanzhou University, Lanzhou 730000, China
email: wangyj@lzu.edu.cn
|
|---|
| |
Dun Zhao
School of Mathematics and Statistics
Gansu Key Laboratory of Applied
Mathematics and Complex Systems
Lanzhou University, Lanzhou 730000, China
email: zhaod@lzu.edu.cn
|
|---|
Return to the EJDE web page
 ,
,
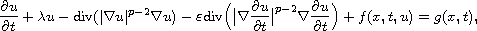
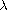 is a positive constant,
is a positive constant,
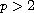 and
and
![$\varepsilon\in(0,1]$](gifs/ae.gif) .
The well-posedness and upper semicontinuity of pullback attractors
are established for the problem without the uniqueness of solutions
under singular perturbations.
.
The well-posedness and upper semicontinuity of pullback attractors
are established for the problem without the uniqueness of solutions
under singular perturbations.
