Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 204, pp. 1-8.
Poincare inequality and Campanato estimates
for weak solutions of parabolic equations
Junichi Aramaki
Abstract:
We shall show that the Poincare type inequality holds for the
weak solution of a parabolic equation. The key is to control the
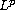 norm of the first derivative of the weak solution with respect to
the time variable. The inequality is necessary to get an estimate in
the Campanato space
norm of the first derivative of the weak solution with respect to
the time variable. The inequality is necessary to get an estimate in
the Campanato space
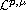 for general parabolic equations.
for general parabolic equations.
Submitted December 24, 2015. Published July 28, 2016.
Math Subject Classifications: 35A09, 35K10, 35D35.
Key Words: Poincare type inequality; weak solution; parabolic equation.
Show me the PDF file (188 KB),
TEX file for this article.
 |
Junichi Aramaki
Division of Science
Faculty of Science and Engineering
Tokyo Denki University
Hatoyama-machi, Saitama 350-0394, Japan
email: aramaki@mail.dendai.ac.jp
|
|---|
Return to the EJDE web page
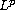 norm of the first derivative of the weak solution with respect to
the time variable. The inequality is necessary to get an estimate in
the Campanato space
norm of the first derivative of the weak solution with respect to
the time variable. The inequality is necessary to get an estimate in
the Campanato space
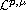 for general parabolic equations.
for general parabolic equations.
