Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 201, pp. 1-11.
Global and local behavior of the bifurcation diagrams
for semilinear problems
Tetsutaro Shibata
Abstract:
We consider the nonlinear eigenvalue problem
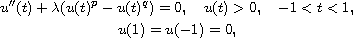
where
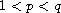 are constants and
are constants and
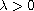 is a parameter.
It is known in [13] that the bifurcation curve
is a parameter.
It is known in [13] that the bifurcation curve
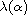 consists of two branches, which are denoted by
consists of two branches, which are denoted by
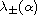 .
Here,
.
Here,
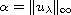 . We establish the
asymptotic behavior of the turning point
. We establish the
asymptotic behavior of the turning point
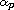 of
of
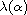 ,
namely, the point which satisfies
,
namely, the point which satisfies
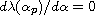 as
as
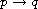 and
and
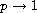 .
We also establish the asymptotic formulas for
.
We also establish the asymptotic formulas for
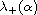 and
and
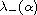 as
as
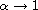 and
and
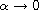 ,
respectively.
,
respectively.
Submitted June 20, 2016. Published July 27, 2016.
Math Subject Classifications: 34F10.
Key Words: Asymptotic behavior; parabola-like bifurcation curves.
Show me the PDF file (244 KB),
TEX file for this article.
 |
Tetsutaro Shibata
Laboratory of Mathematics
Institute of Engineering
Hiroshima University
Higashi-Hiroshima, 739-8527, Japan
email: shibata@amath.hiroshima-u.ac.jp
|
|---|
Return to the EJDE web page
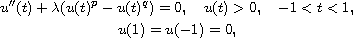
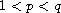 are constants and
are constants and
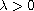 is a parameter.
It is known in [13] that the bifurcation curve
is a parameter.
It is known in [13] that the bifurcation curve
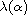 consists of two branches, which are denoted by
consists of two branches, which are denoted by
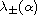 .
Here,
.
Here,
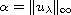 . We establish the
asymptotic behavior of the turning point
. We establish the
asymptotic behavior of the turning point
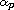 of
of
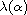 ,
namely, the point which satisfies
,
namely, the point which satisfies
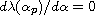 as
as
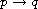 and
and
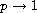 .
We also establish the asymptotic formulas for
.
We also establish the asymptotic formulas for
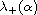 and
and
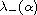 as
as
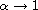 and
and
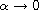 ,
respectively.
,
respectively.
