Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 191, pp. 1-16.
Existence of nonnegative solutions for singular elliptic problems
Tomas Godoy, Alfredo J. Guerin
Abstract:
We prove the existence of nonnegative nontrivial weak solutions to the problem
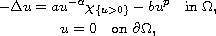
where
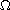 is a bounded domain in
is a bounded domain in
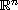 .
A sufficient condition for the existence of a
continuous and strictly positive weak solution is also given, and the
uniqueness of such a solution is proved. We also prove a maximality property
for solutions that are positive a.e. in
.
A sufficient condition for the existence of a
continuous and strictly positive weak solution is also given, and the
uniqueness of such a solution is proved. We also prove a maximality property
for solutions that are positive a.e. in
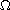 .
.
Submitted March 8, 2016. Published July 13, 2016.
Math Subject Classifications: 35J75, 35D30, 35J20.
Key Words: Singular elliptic problem; variational problems; nonnegative solution;
positive solution; sub-supersolution.
Show me the PDF file (294 KB),
TEX file for this article.
 |
Tomas Godoy
FaMAF, Universidad Nacional de Córdoba
Ciudad Universitaria, 5000
Córdoba, Argentina
email: tomasgodo@gmail.com
|
|---|
| |
Alfredo J. Guerin
FaMAF, Universidad Nacional de Córdoba
Ciudad Universitaria, 5000
Córdoba, Argentina
email: guerin.alfredojose@gmail.com
|
|---|
Return to the EJDE web page
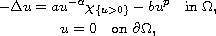
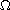 is a bounded domain in
is a bounded domain in
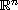 .
A sufficient condition for the existence of a
continuous and strictly positive weak solution is also given, and the
uniqueness of such a solution is proved. We also prove a maximality property
for solutions that are positive a.e. in
.
A sufficient condition for the existence of a
continuous and strictly positive weak solution is also given, and the
uniqueness of such a solution is proved. We also prove a maximality property
for solutions that are positive a.e. in
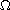 .
.
