Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 190, pp. 1-8.
A waveless free surface flow past a submerged triangular obstacle
in presence of surface tension
Hakima Sekhri, Fairouz Guechi, Hocine Mekias
Abstract:
We consider the Free surface flows passing a submerged triangular obstacle
at the bottom of a channel. The problem is characterized
by a nonlinear boundary condition on the surface of unknown
configuration. The analytical exact solutions for these problems
are not known. Following Dias and Vanden Broeck [6],
we computed numerically the solutions via a series truncation method.
These solutions depend on two parameters: the Weber number
 characterizing the strength of the surface tension and the angle
characterizing the strength of the surface tension and the angle
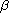 at the base characterizing the shape of the apex.
Although free surface flows with surface tension admit capillary waves,
it is found that solution exist only for values of the Weber number greater
than
at the base characterizing the shape of the apex.
Although free surface flows with surface tension admit capillary waves,
it is found that solution exist only for values of the Weber number greater
than
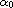 for different configurations of the triangular obstacle.
for different configurations of the triangular obstacle.
Submitted November 5, 2015. Published July 13, 2016.
Math Subject Classifications: 35B40, 35Q35, 76B07, 76D45, 76M40.
Key Words: Free surface; potential flow; Weber number;
surface tension; nonlinear boundary condition.
Show me the PDF file (293 KB),
TEX file for this article.
Hakima Sekhri
Department of Mathematics, Faculty of sciences
University Setif1.19000, Algeria
email: sekhrihakima@yahoo.fr
|
Fairouz Guechi
Department of Mathematics, Faculty of sciences
University Setif1.19000, Algeria
email: f_guechi@yahoo.fr
|
Hocine Mekias
Department of Mathematics, Faculty of sciences
University Setif1.19000, Algeria
email: mekho58@gmail.com
|
Return to the EJDE web page
 characterizing the strength of the surface tension and the angle
characterizing the strength of the surface tension and the angle
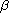 at the base characterizing the shape of the apex.
Although free surface flows with surface tension admit capillary waves,
it is found that solution exist only for values of the Weber number greater
than
at the base characterizing the shape of the apex.
Although free surface flows with surface tension admit capillary waves,
it is found that solution exist only for values of the Weber number greater
than
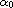 for different configurations of the triangular obstacle.
for different configurations of the triangular obstacle.